Archimedean Solids

Secret origin to the golden ratio found in the Thirteenth Archimedean Solid

Buckminster Fuller was so nice to me. When in college, I showed him my math on the Twelfth Archimedean Solid. I thought it was amazing this solid's volume to be exactly 95 + 50√5. Plotted here as the 9vT volume point. The Twelfth Archimedean is also called the Great Rhombicosidodecahedron. Dome builders use the term Triacon for breakdown types in which new struts are perpendicular to original ones.

An eloquent expositor in all areas of geometry, Harold S. M Coxeter, was first to solve the Snub Dodecahedron. His friend, Eric Weisstein, helped me with understanding Uniform Polyhedra. I sent my book to Donald Coxeter and we talked. I became friends with Harish Rajpoot when he was at Madan Mohan Malaviya University of Technology, Gorakhpur, where the Rapti runs down from Nepal.

The other two closed form solutions of the Snub Dodecahedron are in an essay coauthored with Menno Kosters. At the bottom of this wiki page, Snub Dodecahedron, there is a link to this essay, as is linked below. Menno is the owner of this Wikipedia page and an advocate of SageMath. In the essay, he uses SageMath to solve the volume of the Snub Dodecahedron. This solid is thirteenth on the list given by Pappus in his Fifth book of the Collection.

One rainy night in the early 1980’s, I was sleeping in my car at a lighthouse somewhere above San Francisco. I had programmed my HP calculator to numerically solve the Thirteenth. I woke up and tried √3 sin α-cos α, to my astonishment, it was equal to the edge distance, D.

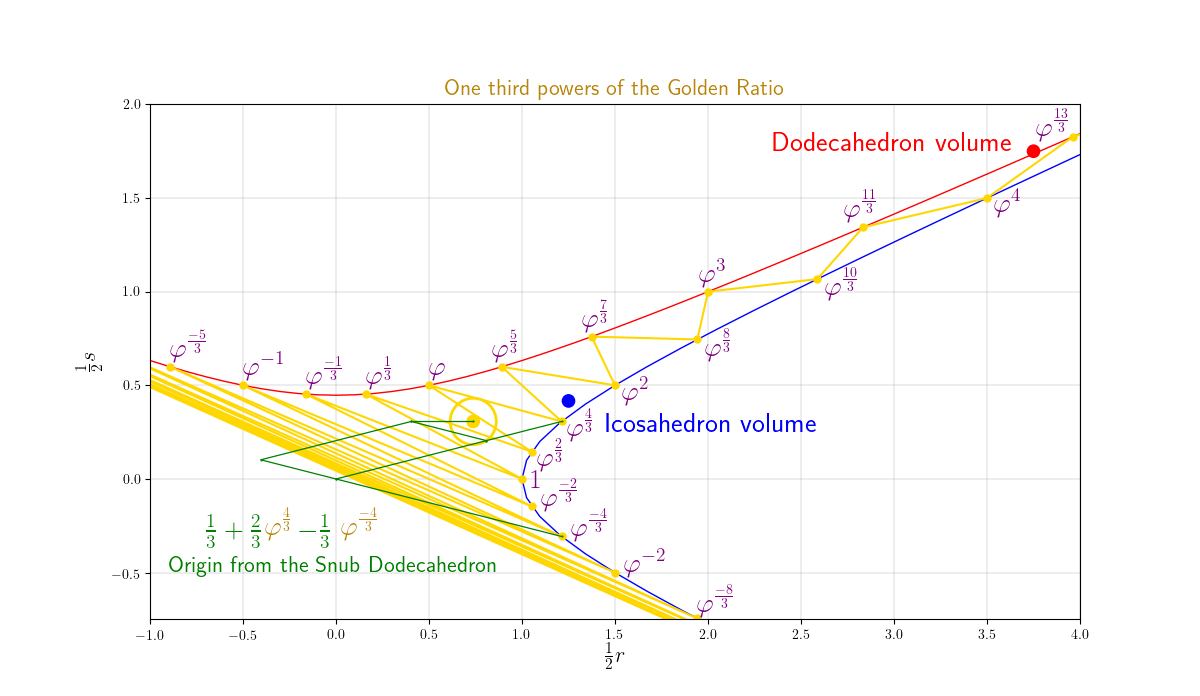
So, Menno and me wrote Volume Solutions to the Snub Dodecahedron which reveals a secret origin to the golden ratio found in the Thirteenth Archimedean. Fuller's spinnability of negative and positive leads to a new root, as shown above, what appears to be an Origin to One third powers of the Golden Ratio!.